DSP:MFCC计算
MCFF(Mel Frequency Cepstrum Coefficient)的计算过程、背景以及相应的python代码。
MFCC:考虑了人的听觉系统特性,将线性频谱映射到基于听觉感知特性的 Mel 频谱上,然后再计算倒谱。声道的 shape 表现为短时间功率谱的包络线(envelope of the short time power spectrum),MFCCs 的工作则是如何准确地表征这种 envelope。
1. 人听觉系统的特性
人听到的声音高低和声音频率不成线性关系,而是成对数关系。
屏蔽效应:人不能听到所有的声音,只有两个频率分量相差一定的带宽时,人耳才能区分。否则只有听到一个音调。这个带宽称为临界带宽:
- 其中$f_c$为中心频率。
- 当$f_c$在 1kHz 以下时,临界带宽基本恒定为 100Hz。
- 当$f_c$在 1kHz 以上时,临界带宽呈指数增加。
模拟上述的听觉特性,可以进行构造模仿人耳的感知特性。
- Mel 频率尺度:对数关系
- Mel 滤波器组:屏蔽效应
- 每一个滤波器的中心频率在 mel 频率域中呈等间隔分布
- 每一个滤波器的带宽在其临界带宽范围内
2. MFCC的计算步骤
- 输入语音信号 — 语音波谱
- 预加重、分帧、加窗 — 分为不同帧的语音波谱
- 用 FFT 计算信号频谱 — 不同帧对应的频谱
- 计算频谱的绝对值/平方 — 不同帧对应的能量谱
- 使用 Mel 滤波器组 — 获得更符合人类听觉的 Mel 谱特征
- 取对数 — 为了倒谱做准备
- DCT — 将乘积通过对数转化为加法。
- Delta MFCC
- 输出语音特征
2.1 预加重、分帧、加窗
2.1.1 预加重
即通过一个高通滤波器。在时域中写为:
预加重的目的是使频谱变得平坦。同时,也是为了消除发生过程中声带和嘴唇的效应,来补偿语音信号受到发音系统所抑制的高频部分,也为了突出高频的共振峰。$\mu$的取值一般为 0.9~1 之间。
2.1.2 分帧
一个窗为一帧。通常情况下 N=256,时间为 20ms~30ms。对于 8kHz 的信号来说,若帧长度为 256 个采样点,则对应的时间为$256 / 8000\times 1000 = 32ms$。
2.1.3 加窗
对每一帧使用汉明窗。通常,$a$取值为 0.46.
2.2 FFT
对每一帧进行 FFT,变换到频率域中。
2.3 Mel滤波器组
人的听力像是一组滤波器(见第一节讨论的屏蔽效应),听见的声音在频谱上是不连续的;并且在低频上分布更密集(同样参见第一节中人听到的声音特性)。将能量谱通过一组 Mel 尺度的三角形滤波器组,定义一个有 $M$ 个滤波器的滤波器组。
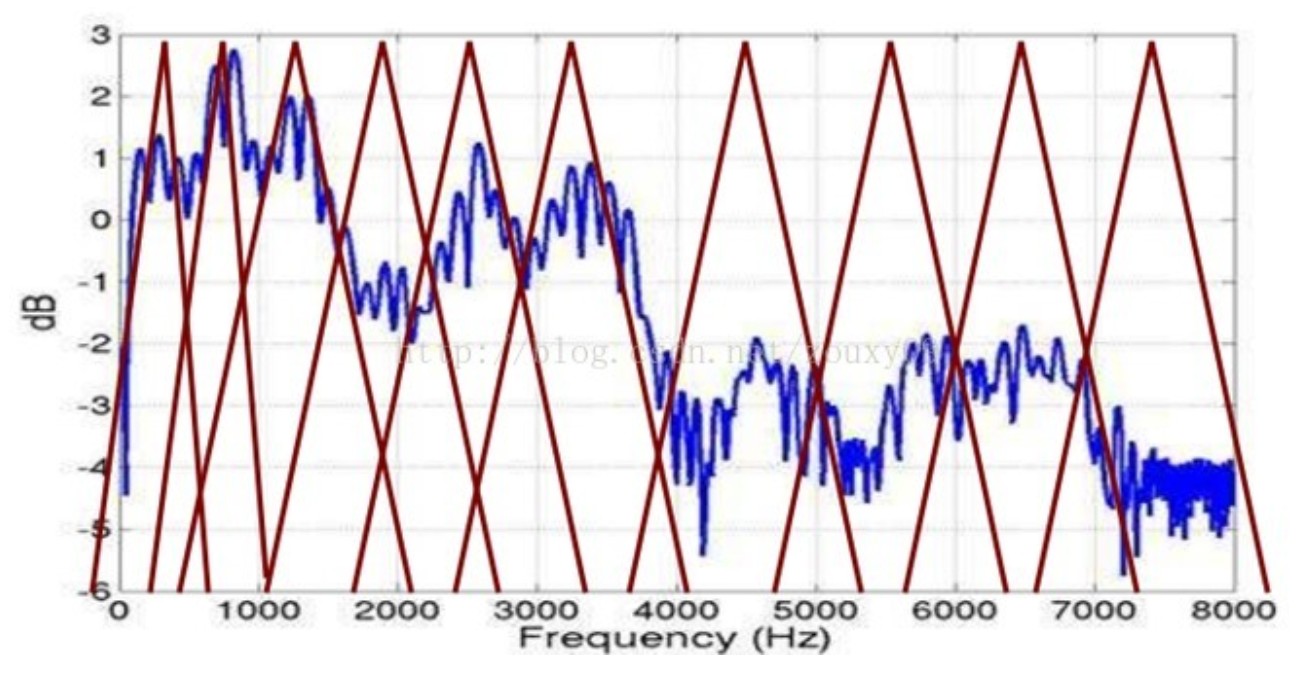
- 中心频率$f_c(l)$在 Mel 频率域中是等间隔分布
- 每一个滤波器的中心频率为:其中:$N$为窗口宽度,$F_s$为采样频率,$M$为滤波器数量,通常取 22~26。通过上式可以获得 M 个带通滤波器$H_m(k)$
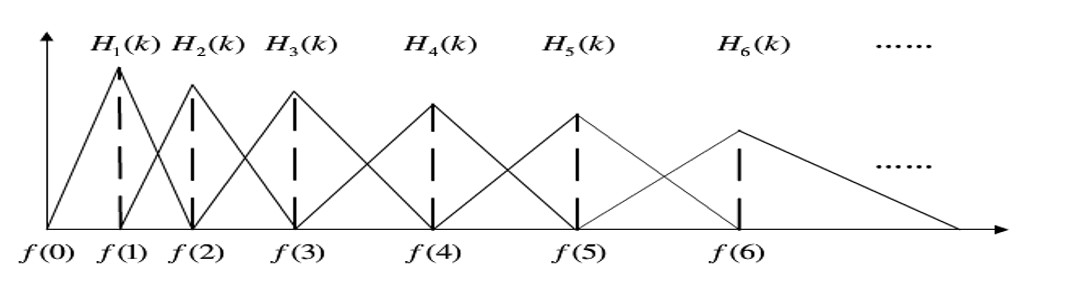
对频谱进行平滑化,并消除谐波的作用,突显原先语音的共振峰。因此一段语音的音调或音高,是不会呈现在 MFCC 参数内,换句话说,以 MFCC 为特征的语音辨识系统,并不会受到输入语音的音调不同的影响。此外,还可以降低运算量。
计算每个滤波器组输出的对数能量。其中$M$为滤波器个数,$N$为窗口大小。
2.4 离散馀弦变换(DCT)
对滤波器组输出$S(m)$,DCT 得到 Mel 频率的倒谱系数$c(n)$。
DCT 正变换:
DCT 反变换:
将$S(m)$作为上式中的$f(x)$,$m$作为$x$得到下式:
这里的$L$是 MFCC 系数的阶数,通常取 12~16。
2.5 Delta MFCC
到此为止,MFCC 只是获得了当前帧的语音特征。而相邻帧之间是连续的,可以通过相邻帧之间的变化更好地表达语音的特征。
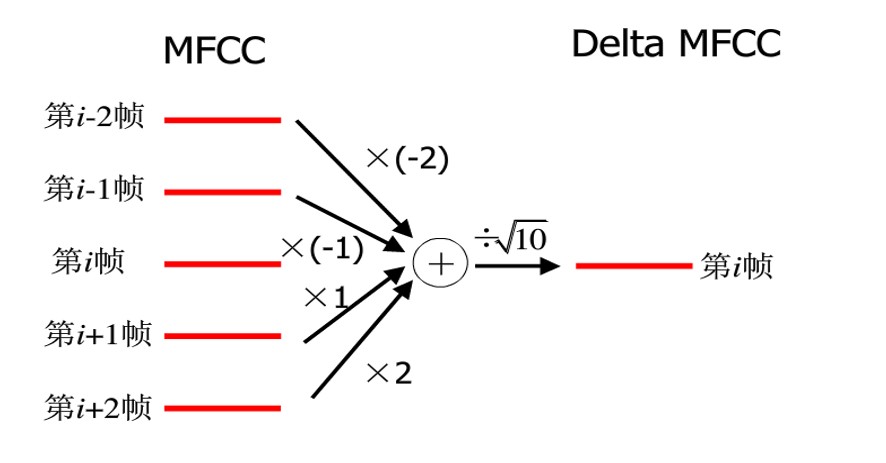
3. MFCC常用参数集
| 参数 | 取值 |
|---|---|
| $\mu$(预加重参数) | 0.9~1 |
| $N$(窗口大小) | 256/512 |
| 采样率 | 8kHz/16kHz |
| 帧长 | 20ms~30ms |
| $M$(Mel 滤波器组数量) | 22~26 |
| $L$(MFCC 阶数) | 12~16 |
| $a$(汉明窗系数) | 0.46 |
4. 参考
- 这篇文章将原理解释得挺不错:梅尔频率倒谱系数(MFCC)
- 这篇将流程解释得更清楚:语音特征 MFCC 提取过程详解