语音频谱处理

• 叠加原理
• 卷积同态系统
• 复倒谱和倒谱
• 复倒谱的计算
• 语音信号的倒谱分析
• 计算 MFCC 系数

1. 广义叠加原理

对于线性系统，使用卷积或者乘法代替线性系统的叠加原理，即：

$$H[x(n)]=H[x_1(n)*x_2(n)]=H[x_1(n)*x_2(n)]=y_1(n)*y_2(n)=y(n)$$

2. 卷积同态系统

卷积同态系统由三部分组成：

• 特征系统：$D_*[]$
• 线性系统：$L[]$
• 逆特征系统：$D_*^{-1}[]$

$D_*[]$
输入是若干信号的卷积，输出为若干信号的加法组合。有以下的特性

$$D_*[x(n)]=D_*[x_1(n)*x_2(n)]=D_*[x_1(n)]+D_*[x_2(n)]=\hat{x}_1(n)+\hat{x}_2(n)=\hat{x}(n)$$

$L[]$
服从叠加原理：

$$L[\hat{x}(n)]=L[\hat{x}_1(n)+\hat{x}_2(n)]=L[\hat{x}_1(n)]+L[\hat{x}_2(n)]=\hat{y}_1(n)+\hat{y}_2(n)=\hat{y}(n)$$

$D_*^{-1}[]$
变换回卷积组合：

$$D_*^{-1}[\hat{y}(n)]=y(n)$$

卷积同态的实现方法。利用 Z 变换，可以将卷积组合变为乘法，利用对数特性，将乘法组合变为加法，用此构成同态系统的特征系统$D_*[]$。其逆同态则是将取对数转化为指数运算。

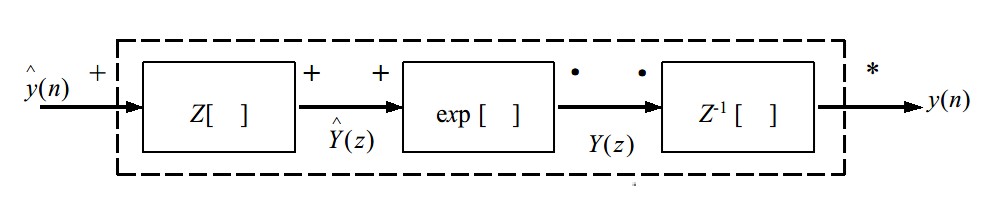
同态系统的用途

• 将二个信号通过卷积（或乘积）合成的信号分开，是一种非线性处理方法。
• 对语音信号来说，同态处理的目的是将激励和声道分开，然后再分别进行研究
  • 对激励进行研究，可以确定语音片段是清音、浊音及浊音的基音频率等特征
  • 对声道进行研究，可以确定声道特性及共振峰等特征

3. 复倒谱和倒谱

设信号$x(n)$的 Z 变换为$X(z)$，其对数为$\hat{X}(z)=lnX(z)=ln[z[x(n)]]$。
那么$\hat{X}(z)$的逆变换为$\hat{x}(n)=z^{-1}[\hat{X}(z)]=z^{-1}[lnz[x(n)]]$

复对数的多值性问题
在复倒谱分析中，Z 变换得到的是复数，所以取对数涉及复对数运算，存在相位多值性问题，称为相位卷绕。

例如：对于a为正实数，b为负实数，$ln(ab)=ln(a|b|e^{jk\pi})=ln(a)+ln(|b|)+jk\pi$。

在计算复倒谱时，应保证复对数函数的单值性，满足广义叠加原理，且要选定收敛域以保证逆 z 变换的唯一性。

注意
在计算倒谱的情况下，信号经过同态处理的正、逆特征系统后，不能还原自身！因为此时只有幅值信息，丢掉了相位信息。对语音信号分析来说，因为人的听觉系统对频谱幅值敏感，对相位不敏感，所以倒谱分析可以用于语音信号。

如果对$X(e^{jw})$的绝对值取对数，得

$$\hat{X}(e^{jw})=ln|X(e^{jw})|$$

求出的倒谱频称为实倒谱，即

$$c(n)=\frac{1}{2\pi}\int^{\pi}_{-\pi}ln|X(e^{jw})|e^{jwn}$$

4 复倒谱的计算方法

设信号为$x(n)=x_1(n)*x_2(n)$，
则其傅里叶变换：

$$X(e^{jw})=lnX_1(e^{jw})+lnX_2(e^{jw})$$

其幅度为：

$$ln|X(e^{jw})| =ln|X_1(e^{jw})|+ln|X_2(e^{jw})|$$

相位：

$$\phi(w)=\phi_1(w)+\phi_2(w)$$

这被称为相位缠绕。

4.1 微分法

信号$X(n)$和倒频谱$\hat{x}(n)$的计算方法：

$$j\frac{d}{dw}X(e^{jw})=\sum nx(n)e^{-jwn}$$ $$j\frac{d}{dw}\hat{X}(e^{jw})=\sum n\hat{x}(n)e^{-jwn}$$ $$\hat{X}(e^{jw})=lnX(e^{jw})$$

有：

$$\begin{aligned} j\frac{d}{dw}\hat{X}(e^{jw}) &= j\frac{d}{dw}[lnX(e^{jw})]\\ &= \frac{j\frac{d}{dw}[X(e^{jw})]}{X(e^{jw})}\\ &=\sum n\hat{x}(n)e^{-jwn} \end{aligned}$$

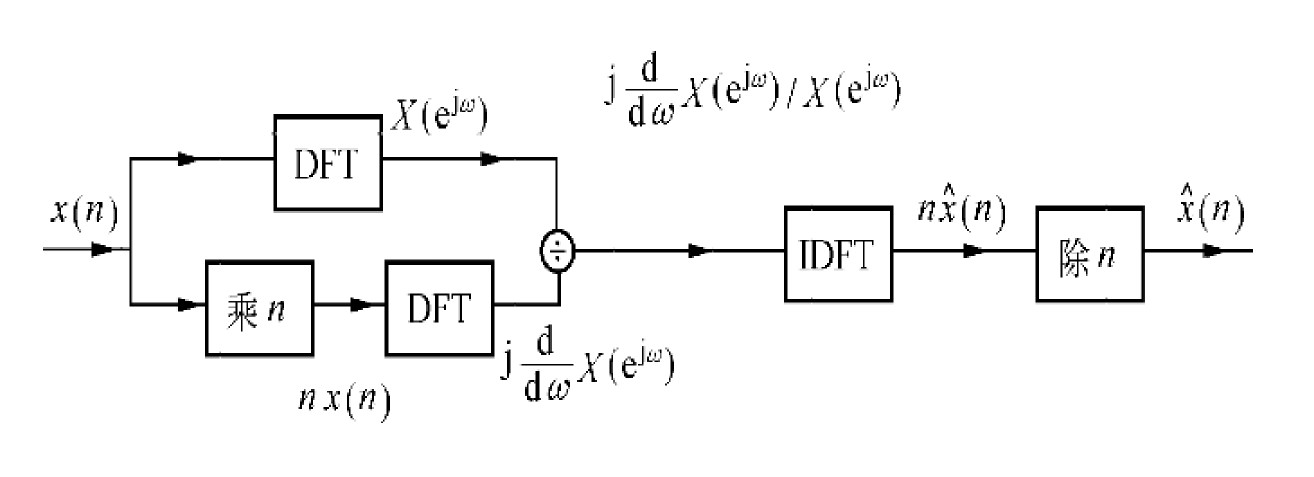
这样就避开了复对数运算。但缺点是，$nx(n)$的高频分量较$X(n)$更多，按照原采样频率进行分析回导致频率混叠问题。

4.2 最小相位信号法

被处理的信号$x(n)$是最小相位信号：Z 变换的全部几点和零点都位于 Z 平面单位元内部的信号，本质上是指具有最小相位延迟的序列信号。在实际应用中，许多信号是最小相位信号，或可以看作是最小相位信号。语音信号的模型就是极点都在 z 平面单位圆内的全极点模型，或者极零点都在 z 平面单位圆内的极零点模型。

设$x(n)$为最小相位信号，则$\hat{x}(n)$为因果稳定序列。

$$\hat{x}(n)=\hat{x}_e(n)+\hat{x}_o(n)$$ $$\hat{x}_e(n)=\frac{1}{2}[\hat{x}(n)+\hat{x}(-n)]$$

则有：

$$\Phi[\hat{x}_e(n)]=\frac{1}{2}[\hat{X}(e^{jw})+\hat{X}(e^{-jw})]=\hat{X}_R(e^{jw})$$

该式不包含相位信息。

注：原序列的实偶对称序列的傅里叶变换等于原序列的傅里叶变换的实部。

$$\begin{aligned} \hat{X}(e^(jw)) &= \hat{X}_R(e^{jw})+j\hat{X}_I(e^{jw})\\ &= ln|X(e^{jw})|+j{arg[X(e^{jw})]+2k\pi}\\ \end{aligned}$$

则$ln|X(e^{jw})| =\Phi[\hat{x}_e(n)]$。
又由于：$\hat{x}_e(n)=\frac{1}{2}[\hat{x}(n)+\hat{x}(-n)]$且$\hat{x}(n)$是一个因果序列，可得

$$\hat{x}(n)=\left\{ \begin{aligned} 0,~~~n<0 \\ \hat{x}_e(n),~~~n=0\\ 2\hat{x}_e(n), ~~~n>0 \end{aligned} \right.$$ 最小相位法求复倒谱原理

5. 语音信号的倒谱分析

根据语音信号产生的线性模型，语音信号由激励信号与声道冲激响应卷积产生的，解卷积就是将卷积分量分开，可采用同态解卷积的方法。

语音信号 -> 同态解卷积分析 -> 分离出激励信号和声道冲激信号相应

• 对声门激励信号进行分析，以判断浊音、清音以及浊音的基音频率
• 对声道冲激响应进行分析，以判断声道特性及共振峰

5.1 声门激励信号的倒谱
声门激励信号（浊音）：$e(n)=\sum_{r=0}^M\alpha_r\delta(n-rN_P)$
对其进行Z变换得：

$$E(z)=\alpha_0\Pi_{r=1}^M[1-\beta_r(z^{N_P})^{-1}]$$

* 此处的$\beta 可以通过\alpha 求得$

$$\hat{E}(z)=ln[E(z)]=ln\alpha_0-\sum_{r=1}^M[-\sum_{k=1}^{\infty}\frac{\beta_r^k}{k}(z^{N_P})^{-k}]$$

求 z 反变换获得倒谱：

$$\hat{e}(n)=loga_0\delta(n)+\sum_{k=1}^{\infty}\beta'_k\delta(n-kN_P)$$

一个周期冲激的有限长度序列，其倒谱也是周期冲激序列，且周期长度是$N_P$不变，只是信号长度成为无限长，振幅随 k 增加而衰减。当声门激励为浊音时，其倒谱只在$kN_P$诸点上不等于 0，其它均为零，那么第一个非零点和原点的距离就是基音周期。

5.2 声道冲激响应的倒谱
用极零点模型描述声道响应，其 Z 变换如下：

$$X(z)=Az^{-r}\frac{\Pi^{M_i}_{k=1}(1-a_kz^{-1})\Pi_{k=1}^{M_o}(1-b_kz)}{\Pi^{N_i}_{k=1}(1-c_kz^{-1})\Pi_{k=1}^{N_o}(1-d_kz)}$$

a, c为单位圆内零极点；反之为单位圆外零极点。$z^{-r}$：序列相对于时间原点的延迟。
单位圆内的零极点形成复倒谱的右边；单位圆外的零极点形成复倒谱的左边；在原点的值取决于增益。复倒谱通常是双边的，且是比例因子为1/n的衰减指数之和。
$\hat{X}(z)$的复对数为：

$$\hat{X}(z)=ln(A)+ln(z^{-r})+\sum_{k=1}^{M_i}ln(1-a_kz^{-1})+\sum_{k=1}^{M_o}ln(1-b_kz^{-1})\\-\sum_{k=1}^{N_i}ln(1-c_kz^{-1})-\sum_{k=1}^{N_o}ln(1-d_kz^{-1})$$

我们希望上式逆 Z 变换是稳定序列，即绝对可求和，即使ROC包括单位圆。$\hat{X}(z)$的 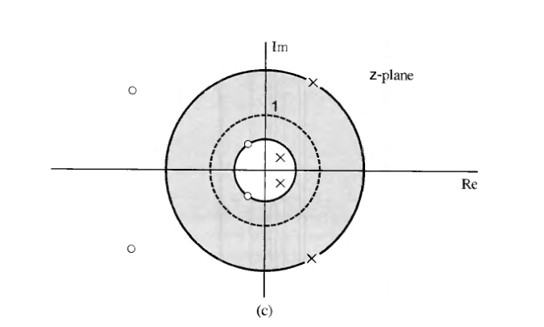RoC：

Roc

其复倒谱：

$$\hat{x}(n)=\left\{ \begin{aligned} ln[A],~~~n=0 \\ \sum_{k=1}^{N_i}\frac{c_k^n}{n}-\sum_{k=1}^{M_i}\frac{a_k^n}{n},~~~n>0\\ \sum_{k=1}^{M_o}\frac{b_k^{-n}}{n}-\sum_{k=1}^{N_o}\frac{d_k^{-n}}{n}, ~~~n<0 \end{aligned} \right.$$

6. 基于听觉特征的MEL频率倒谱系数

一种常用的语音特征：MFCC （mel frequency cepstrum coefficient）

人耳能在嘈杂的环境中分辨各种声音 -> 耳蜗起到重要作用 ->耳蜗相当于滤波器组 ->作用：在对数频率尺度上进行滤波 ->对低频信号敏感。基于上述原理，得到类似与耳蜗的滤波器组：Mel 频率滤波器组。Mel 频率：$f_{mel}=2595\times log(1+f/700)$

MFCC 计算:

• 分帧 -> 预加重 -> 加汉明窗 -> 短时傅里叶变换 -> 得到频谱；
• 求频谱平方，即能量谱，用 M 个 Mel 带通滤波器进行滤波；
• 对每个滤波器的输出取对数，得到相应频带的对数功率谱，并进行反离散馀弦变换，得到 L 个 MFCC 系数，一般 L 取 12 ~ 16 个左右。MFCC 系数为： $$C_n=\sum_{k=1}^Mlogx'(k)cos[\pi(l-0.5)n/M],~~~n=1, 2, ..., L$$
• 将直接得到的 MFCC 特征作为静态特征，再做一阶和二阶差分，得到相应的动态特征。